揭秘数学界圣杯：黎曼假设的深层意义与未解之谜

黎曼假设：数学领域的未解之谜

在数学浩瀚的星空中，黎曼假设（或称黎曼猜想）犹如一颗璀璨而神秘的星辰，长久以来吸引着无数数学家的目光与探索。这一由德国数学家波恩哈德·黎曼于1859年提出的假设，不仅在数学界占有举足轻重的地位，更是成为了现代数学研究中的一个核心问题。本文将带您深入了解黎曼假设的含义、重要性及其研究现状，让目标用户能够全面认识这一数学难题。

一、黎曼假设的起源与定义

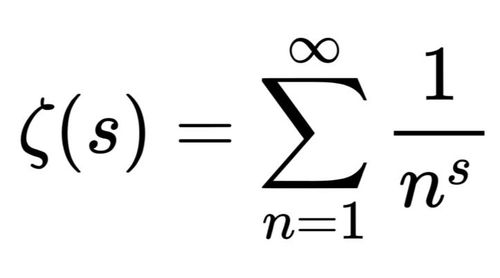
黎曼假设是关于黎曼ζ函数ζ(s)的零点分布的猜想。黎曼ζ函数是一个在复平面上定义的函数，其中s是复数。这个函数在数论和复变函数理论中扮演着重要角色，尤其是与素数分布有着紧密的联系。黎曼在研究中发现，素数的频率与ζ函数的性态之间存在某种神秘的关联。

复平面上使ζ函数取值为零的点被称为ζ函数的零点。根据性质的不同，这些零点可以分为两类：平凡零点和非平凡零点。平凡零点指的是s=-2n（n为正整数）的点，这些零点分布有序、性质简单。而除了这些平凡零点外，ζ函数还有许多其他零点，即非平凡零点，它们的性质更为复杂且难以捉摸。

黎曼假设的具体表述是：ζ函数的所有非平凡零点都位于复平面上实部为1/2的直线上，这条直线被称为临界线（critical line）。即，对于所有的非平凡零点s，都有Re(s)=1/2，其中Re(s)表示复数s的实数部分。

二、黎曼假设的重要性

尽管在知名度上，黎曼假设可能不及费尔马猜想和哥德巴赫猜想，但其在数学上的重要性却远远超过后两者。这一假设不仅是数论和复变函数领域的一个核心问题，其解决还将对这两个领域产生深远的影响。

首先，黎曼假设的解决将为素数分布的研究提供新的视角和方法。素数作为数学中的基本元素，其分布规律一直是数学家们关注的焦点。黎曼ζ函数与素数分布的紧密联系，使得黎曼假设的解决有望揭示素数分布的更深层次规律。

其次，黎曼假设在数学理论的发展中具有重要地位。当今数学文献中已有超过一千条数学命题以黎曼猜想（或其推广形式）的成立为前提。这意味着，如果黎曼假设被证明为真，那么这些数学命题也将得到验证，从而推动数学理论的进一步发展。

此外，黎曼假设还具有重要的科学价值和经济意义。克雷数学研究所将黎曼假设列为千禧年七大数学难题之一，并承诺为解决这一难题的数学家提供100万美元的奖金。这一举措不仅表明了黎曼假设的重要性，也激发了数学家们对这一难题的研究热情。

三、黎曼假设的研究现状

自黎曼提出这一假设以来，已经过去了近170年的时间，但至今尚未有人给出令人信服的证明。然而，数学家们在这一领域的研究取得了不少进展。

首先，已经使用计算机验证了复平面上最初的数十亿个ζ函数的零点，都符合黎曼猜想的排列规律。这一结果虽然无法直接证明黎曼假设的成立，但为后续的研究提供了有力的支持。

其次，数学家们还提出了关于黎曼猜想可能例外数量的新上限。这些研究不仅深化了对黎曼ζ函数非平凡零点性质的理解，也为黎曼猜想的最终解决提供了有益的参考。

此外，还有一些数学家尝试从物理理论中寻找解决黎曼假设的正确途径。他们利用物理学中的概念和方法，对黎曼ζ函数进行深入研究，希望能够找到证明黎曼假设的新思路。例如，现年89岁的阿蒂亚和现年82岁的李忠在证明黎曼假设的过程中就借助了物理概念；前者用上物理学中精细结构常数α，后者用上物理学中Riech度量。然而，这些尝试尚未取得突破性进展。

四、未来的展望

尽管黎曼猜想的解决仍然面临巨大的挑战，但数学家们对其研究的热情并未减退。随着数学理论和计算技术的不断发展，相信未来在黎曼猜想的研究上会有更多的突破和进展。

一方面，随着计算机技术的不断提升，我们可以更加精确地验证更多的ζ函数零点是否满足黎曼猜想的排列规律。这将为我们提供更多关于黎曼ζ函数非平凡零点性质的信息，从而推动研究的深入。

另一方面，数学家们也在不断探索新的数学方法和工具来解决黎曼假设。他们希望通过跨学科的研究合作，将数学与其他学科相结合，从而找到证明黎曼假设的新途径。

总之，黎曼假设作为数学领域的一个重要问题，其解决将对数学理论的发展产生深远的影响。我们期待着未来能够见证这一难题的解决，也期待着数学科学因此注入新的活力和动力。