揭秘斜率与倾斜角的神秘关联

在几何学与数学分析中，斜率与倾斜角是两个紧密相连的概念，它们共同描述了直线在平面上的方向。本文旨在清晰、简洁地阐述这两者之间的关系，同时注重内容的结构性和关键词的合理使用，以提升读者的理解深度和搜索引擎的友好度。

首先，让我们从基本概念入手。斜率（slope），在数学中定义为直线倾斜程度的量度，通常用字母“m”表示。直观上，斜率描述了直线上升或下降的速率。例如，在一条从左下到右上的直线中，斜率为正，表示随着x的增加，y也增加；相反，在一条从左上到右下的直线中，斜率为负，表示随着x的增加，y减少。斜率的计算公式为：m = (y2 - y1) / (x2 - x1)，其中(x1, y1)和(x2, y2)是直线上的任意两点。

倾斜角（angle of inclination），则是直线与其正x轴正向之间所夹的锐角或直角，通常用希腊字母“θ”或“α”表示。在直角坐标系中，倾斜角的大小直接反映了直线的方向。倾斜角的取值范围是0°到180°（不包括180°，因为180°对应的是与x轴负方向重合的直线，此时没有明确的斜率）。值得注意的是，当直线与x轴平行时，倾斜角为0°，斜率也为0；当直线垂直于x轴时，倾斜角为90°，此时斜率不存在（因为分母x2 - x1为0）。

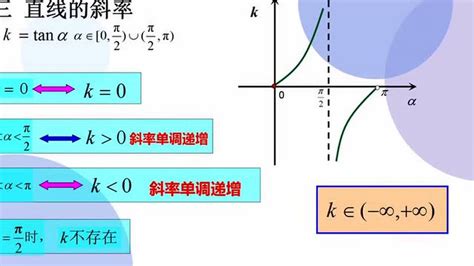
接下来，我们深入探讨斜率与倾斜角之间的数学关系。这一关系可以用一个简单的三角函数表达式来描述：斜率m等于倾斜角θ的正切值，即m = tan(θ)。这个公式是连接斜率与倾斜角的桥梁，它揭示了两者之间的本质联系。

当θ在0°到90°之间时，随着θ的增加，tan(θ)的值也增加，即斜率m增大，表示直线变得更加陡峭。特别地，当θ接近90°时，tan(θ)趋向于无穷大，对应于斜率极大的直线，即几乎垂直于x轴的直线。

当θ在90°到180°之间时，虽然直线的方向仍然是向下倾斜，但在此范围内讨论斜率与倾斜角的关系需要引入负角度的概念或者考虑直线的反向延长线。从数学上讲，此时直线的斜率m为负，且随着θ从90°增加到180°，m的绝对值减小（即斜率的绝对值逐渐变小，但方向仍为负）。

通过上述分析，我们可以发现斜率与倾斜角的关系不仅是一个数学公式，更是对直线方向性的一种直观表达。斜率的正负和大小直接反映了直线的倾斜方向和陡峭程度，而倾斜角则提供了一个更直观的几何视角来理解和描述直线的方向。

在实际应用中，斜率与倾斜角的关系有着广泛的应用。例如，在物理学中，斜率常被用来表示速度、加速度等物理量的变化率；在经济学中，斜率可以用来分析供需曲线的斜率变化对市场均衡的影响；在工程学中，斜率和倾斜角则用于计算坡度、设计道路的倾斜度等。

此外，斜率与倾斜角的关系还是学习微积分的重要基础。在导数的学习中，函数的导数可以看作是函数图像上各点处切线的斜率，这一思想贯穿于微积分的整个学习过程。通过理解斜率与倾斜角的关系，学生可以更好地掌握导数的几何意义，进而深入理解微积分中的许多概念和方法。

在探讨斜率与倾斜角关系的过程中，我们还应注意到一些特殊情况的处理。例如，当直线与x轴平行时（倾斜角为0°），斜率为0，这是一个简单的特例。而当直线垂直于x轴时（倾斜角为90°），斜率不存在，这是因为此时直线的方向完全由y轴决定，与x轴无关。这些特殊情况虽然看似简单，但在理解斜率与倾斜角关系的完整性上却是不可或缺的。

综上所述，斜率与倾斜角作为描述直线方向性的两个关键概念，在数学、物理、经济等多个领域都发挥着重要作用。它们之间的关系可以用一个简单的三角函数表达式来概括，即斜率m等于倾斜角θ的正切值。这一关系不仅揭示了直线倾斜程度的数学本质，还为我们在实际应用中解决相关问题提供了有力的工具。

通过本文的阐述，我们希望能够使读者对斜率与倾斜角的关系有一个清晰而全面的认识。同时，我们也注重了内容的结构性和关键词的合理使用，以期提高读者的阅读体验和搜索引擎的友好度。希望本文能够成为读者在学习斜率与倾斜角关系过程中的一份有益参考。