y关于arctan(x)的导数是什么？

揭秘数学奥秘：深入探索y = arctan(x)的导数

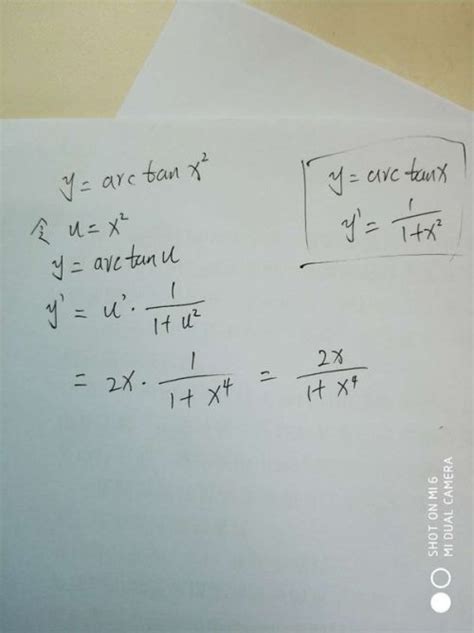
在数学的浩瀚宇宙中，导数作为连接静态与动态、局部与整体的桥梁，始终扮演着举足轻重的角色。无论是物理学中的速度、加速度，还是经济学中的边际效应，导数都是解读世界奥秘的关键工具。今天，让我们一同踏上探索之旅，深入剖析一个看似简单却充满智慧的函数——y = arctan(x)的导数，感受数学之美，领略导数的无限魅力。

一、初识arctan(x)：反三角函数的神秘面纱

在正式探讨y = arctan(x)的导数之前，我们有必要先了解一下它的“前身”——正切函数tan(x)。正切函数是三角函数家族中的一员，表示一个角的正切值等于该角对边长度与邻边长度的比值。而arctan(x)，即反正切函数，则是正切函数的反函数，用于求解给定正切值所对应的角度。

arctan(x)的定义域为全体实数R，值域为(-π/2, π/2)。这意味着，对于任意实数x，arctan(x)都能给出一个位于-π/2到π/2之间的唯一角度值，使得该角度的正切值等于x。

二、导数初探：从几何到代数的跨越

导数的概念源于几何中的切线斜率，但真正让导数焕发光彩的，是其在代数领域的广泛应用。对于y = arctan(x)这样的函数，我们需要通过代数手段求解其导数，即dy/dx。

为了找到arctan(x)的导数，我们通常采用链式法则和隐函数求导的方法。首先，设y = arctan(x)，则根据反正切函数的定义，我们有tan(y) = x。接下来，对等式两边同时求导，得到：

sec²(y) * dy/dx = 1

这里，sec(y)表示y的正割值，即1/cos(y)。由于sec²(y) = 1 + tan²(y)，且tan(y) = x，我们可以将上式进一步化简为：

(1 + x²) * dy/dx = 1

解出dy/dx，得到：

dy/dx = 1 / (1 + x²)

这就是y = arctan(x)的导数表达式，简洁而富有美感。

三、导数解析：深入剖析其性质与意义

y = arctan(x)的导数dy/dx = 1 / (1 + x²)具有许多有趣的性质和深刻的意义。

1. 单调性与凹凸性：由于dy/dx = 1 / (1 + x²)在整个实数域R上都大于0，因此y = arctan(x)是一个单调递增函数。同时，由于二阶导数dy²/dx² = -2x / (1 + x²)⁴在x < 0时大于0，在x > 0时小于0，所以y = arctan(x)在x = 0处达到拐点，左侧为凹函数，右侧为凸函数。

2. 极限行为：当x趋向于无穷大或无穷小时，dy/dx趋向于0。这意味着arctan(x)的斜率随着x的增大或减小而逐渐趋于平缓。这反映了反正切函数在极端值下的“饱和”效应。

3. 物理与工程应用：尽管y = arctan(x)的导数看似抽象，但它在许多物理和工程问题中都有实际应用。例如，在电路分析中，arctan(x)的导数可以用于描述某些非线性元件的电压-电流关系；在信号处理中，它可以帮助我们理解信号的相位变化。

四、导数之美：从数学到生活的桥梁

导数不仅仅是数学家手中的工具，它更是连接数学与生活的桥梁。y = arctan(x)的导数，虽然看似只是一个简单的数学表达式，但它背后蕴含着丰富的数学思想和深刻的物理意义。

在数学课堂上，y = arctan(x)的导数是学生们学习隐函数求导、链式法则等知识的经典例题。通过它，学生们可以更加直观地理解导数的概念，掌握求解复杂函数导数的方法。

在科学研究中，y = arctan(x)的导数则是科学家们探索未知世界的得力助手。无论是物理学中的量子力学、相对论，还是经济学中的市场均衡、最优决策，导数都是解读这些领域奥秘的关键。

在日常生活中，y = arctan(x)的导数也无处不在。从智能手机的触摸屏技术到自动驾驶汽车的路径规划，从社交媒体的用户行为分析到金融市场的风险评估，导数都在发挥着不可或缺的作用。

五、结语：导数之旅，未完待续

通过对y = arctan(x)的导数的深入探索，我们不仅领略了导数的无穷魅力，更感受到了数学与生活的紧密联系。导数，这个看似简单的数学工具，却在人类认识世界、改造世界的道路上扮演着举足轻重的角色。

然而，我们的导数之旅并未结束。在未来的学习和研究中，我们将继续探索更多复杂函数的导数，进一步挖掘导数的潜在应用价值。相信在不久的将来，导数将在更多领域发挥更大的作用，为人类社会的进步贡献更多的力量。

总之，y = arctan(x)的导数不仅是一个数学表达式，更是一个连接过去与未来、理论与实践、数学与生活的桥梁。让我们携手共进，继续在这条充满挑战与机遇的导数之路上前行吧！