高等数学高斯公式到电磁学高斯定理的桥梁

在科学与数学的浩瀚星空中，高斯的名字犹如一颗璀璨的星辰，以其卓越的智慧和贡献照亮了多个领域。从高等数学中的高斯公式到电磁学中的高斯定理，他的名字不仅代表了数学的严谨与美感，也体现了物理学中电场与电荷之间深刻而简洁的关系。本文旨在通俗易懂地介绍这一跨越数学与物理两大领域的理论桥梁，让我们一同探索从高斯公式到高斯定理的奇妙之旅。

高等数学中的高斯公式

高斯公式，又称为高斯-奥斯特罗格拉德斯基公式或散度定理，是矢量分析中的一颗明珠。这个定理在三维空间中描述了一个矢量场通过一个封闭曲面的流量与该矢量场在曲面内部散度的体积积分之间的关系。简单来说，它告诉我们：一个矢量场从一个封闭曲面流出的总量，等于这个矢量场在曲面内部所有点的散度之和。

数学上，高斯公式可以表达为：

\[

\iint_S \vec{F} \cdot d\vec{S} = \iiint_V \nabla \cdot \vec{F} \, dV

\]

其中，\(S\) 表示封闭曲面，\(V\) 表示曲面所包围的体积，\(\vec{F}\) 是矢量场，\(d\vec{S}\) 是曲面上的微小面积向量，\(\nabla \cdot \vec{F}\) 是矢量场的散度，\(dV\) 是体积元素。

这个公式在流体力学、热力学等多个领域有着广泛的应用，它帮助我们理解流体的流动、热量的传递等现象。比如，可以想象一个装满水的容器，水从容器壁流出的总量正好等于容器内部水的增加或减少速率（即散度）在整个体积上的积分。

电磁学中的高斯定理

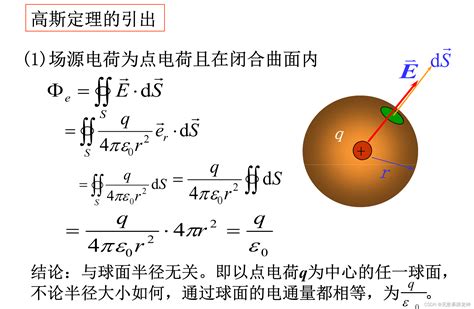
当我们将视线转向电磁学，高斯的名字再次闪耀。高斯定理，也称为高斯通量理论或高斯定律，是静电学中的基本定理之一。它描述了一个封闭曲面穿过电场的总电通量与该曲面内电荷的代数和之间的关系。简单来说，高斯定理告诉我们：电场通过一个封闭曲面的电通量等于该曲面内所有电荷的总和与真空介电常数之比。

数学上，高斯定理可以表达为：

\[

\oint_S \vec{E} \cdot d\vec{A} = \frac{Q_{\text{encl}}}{\epsilon_0}

\]

其中，\(S\) 表示封闭曲面，\(\vec{E}\) 是电场强度，\(d\vec{A}\) 是曲面上的微小面积向量，\(Q_{\text{encl}}\) 是曲面内的总电荷，\(\epsilon_0\) 是真空介电常数。

这个定理揭示了电场分布与电荷分布之间的深刻联系。想象一个充满电荷的空间，我们用一个封闭曲面将其包围，电场线从这个曲面穿过的总量（即电通量）正比于曲面内的电荷总和。这意味着，如果我们知道了电场在一个封闭曲面上的通量，就可以推断出曲面内电荷的分布情况。

从高斯公式到高斯定理：数学与物理的桥梁

尽管高斯公式和高斯定理分别属于数学和物理两个领域，但它们之间却存在着深刻的联系。这种联系体现在它们共同描述了一种“流量”与“源”之间的关系。在数学中，高斯公式描述了一个矢量场通过一个封闭曲面的流量与该矢量场在曲面内部散度的关系；在物理中，高斯定理则描述了一个电场通过一个封闭曲面的电通量与该曲面内电荷的关系。

从更深层次上看，这种联系源于自然界中普遍存在的平方反比律。无论是引力场、电场还是磁场，它们都遵循平方反比律，即场的强度与源的距离的平方成反比。高斯公式和高斯定理正是这种平方反比律在数学和物理中的具体体现。

高斯定理的应用与意义

高斯定理在电磁学中有着广泛的应用。它不仅可以用于计算电荷分布产生的电场，还可以根据测量的电通量来推断电荷分布。这为电场分析提供了一种重要的工具，有助于我们理解电场与电荷之间的相互作用。

例如，在静电场中，我们可以利用高斯定理来计算一个均匀带电球体或均匀带电圆柱的电场分布。由于这些几何形状具有较高的对称性，使得高斯定理的应用变得相对简单。通过选择一个合适的封闭曲面（如球体或圆柱面），我们可以计算出电场在这些曲面上的通量，进而推断出电场分布。

此外，高斯定理还揭示了静电场的一个基本特性：静电场是有源场。这意味着电场线总是从正电荷出发，终止于负电荷。这一特性与磁场形成鲜明对比，因为磁场是无源场，磁场线总是闭合的。

从理论到实践：高斯定理的启示

高斯定理不仅是一个理论上的重要定理，它还在实践中发挥着重要作用。在电力工程中，我们需要计算各种电气设备周围的电场分布，以确保设备的安全运行。高斯定理为我们提供了一种有效的方法来计算这些电场分布。

在材料科学中，高斯定理也扮演着重要角色。当电场作用于材料时，材料内部的电荷分布会发生变化，从而产生极化现象。通过测量电场在材料表面的通量，我们可以推断出材料内部的极化电荷分布，进而了解材料的电学性质。

结语

从高等数学中的高斯公式到电磁学中的高斯定理，我们见证了数学与物理之间的紧密联系和深刻互动。高斯公式和高斯定理不仅是我们理解自然界中矢量场和电场的重要工具，更是我们探索未知、推动科学进步的重要力量。它们提醒我们，无论是在数学的抽象世界中还是在物理的现实世界中，都存在着一种普遍的、深刻的规律等待我们去发现和利用。

通过学习和理解高斯公式和高斯定理，我们不仅能够更好地掌握数学和物理的知识，还能够培养我们的逻辑思维能力和创新能力。让我们在科学的道路上继续前行，不断探索和发现更多未知的奥秘。